Solución:
a) Cálculo del área del cuadrado de l = 4 cm :
A

= l2 = (4cm)2 = 16 cm2
b) Cálculo del área del cuadrado de lado l/3:
A? =
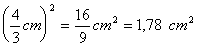
c) Cálculo del área de la región sombreada
Área Sombreada
 =
= 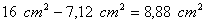
2) Calcular el área de la región sombreada
Solución:
a) Cálculo del área del círculo
b) Cálculo del área del cuadrado
Si el
radio de la circunferencia es 4cm, entonces el lado del cuadrado es 8 cm, es decir, Si

= 4 cm ? l

= 8cm
Entonces el área del cuadrado es:
A

= l2 = (8cm)2 = 64 cm2
c) Cálculo del área de la región sombreada
Se obtiene al restar el área del círculo de la del cuadrado
3) Calcular el área de la región sombreada (sector circular) en donde

cm y el ? tiene un tercio de 3600
Solución:
a) Cálculo del radio r:
Si

?

b) Cálculo del ángulo ??
c) Cálculo del área del sector circular:
4) Calcular el área de la región sombreada (corona circular) en donde

cm .
Solución:
a) Cálculo del radio subdos:
Si

cm ?

b) Cálculo del radio subuno:?
Si

c) Cálculo del área del círculo de radio subdos:
d) Cálculo del área del círculo de radio subuno:
e) Cálculo del área de la corona circular
5) Calcular el área de la región sombreada (trapecio circular) en donde

cm .
Solución:
a) Cálculo del radio subuno:
?

cm
b) Cálculo del radio subuno:
Si

??

c) Cálculo del sector circular de radio subuno:
d) Cálculo del sector circular de radio subdos:
e) Cálculo del área del trapecio circular:
6) De una pizza se ha comido

como indica la figura:
La pizza cabe exactamente en una caja cuadrada que tiene 160 cm de perímetro. Calcular el área y la longitud del arco de la parte comida.
Solución.- Primera forma:
a) Cálculo del lado de la caja cuadrada
b) Cálculo del radio de la pizza
Si

Si

c) Cálculo del área total de la pizza
d) Cálculo del área de la parte comida
Como la parte comida es


de la pizza,
Entonces:
e) Cálculo del perímetro de la pizza
f) Cálculo de la longitud del arco de la parte comida
Solución.- Segunda forma:
a) Cálculo del lado de la caja cuadrada
b) Cálculo del radio de la pizza
Si

Si

c) Cálculo del ángulo ?
d) Cálculo del área de la parte comida
e) Cálculo de la longitud del arco de la parte comida
Nota: Recuerde que tanto en
Matemática como en la vida diaria el mismo problema tiene varias formas de solución. En este contexto, la Matemática cumple un rol estratégico, ya que esta
ciencia permite ver
soluciones en donde otros no observan.
7) Calcular el área de la región sombreada en donde d
= 
cm y b =

cm.
Solución:
a) Cálculo de la diagonal:
Si d
= 
cm ?

b) Cálculo de la base:
Si b =

cm??

c) Cálculo de la altura aplicando el Teorema de Pitágoras:
d) Cálculo del área de la región pintada, la misma que es un triángulo:
A
 =
= 
9) Si d =

cm. Calcular el área de la región sombreada
Solución:
a) Cálculo de la diagonal
Si d =

cm ?

b) Cálculo del lado del cuadrado
Por Pitágoras

c) Cálculo del área del cuadrado
d) Cálculo del área del triángulo sin sombrear
e) Cálculo del área sombreada
1) ¿El área de un rectángulo equilátero cuya diagonal mide 2 cm es?
a) 2 cm2
|
b)4 cm2
|
c) 1 cm2
|
d) 3 cm2
|
a)
2) El área de la figura es:
a) 10 cm2
|
b) 12 cm2
|
c) 14 cm2
|
d) 16 cm2
b)
|
3) En la figura se tiene un cuadrado de lado 2a. En las esquinas se tiene 4 cuadrados de lado a/2, entonces el área sombreada es:
a) 2 a2
|
b) 3 a2
|
c) 6 a2
|
d) 8 a2
b)
|
4) El centro de un cuadrado de 2 cm de lado coincide en el vértice de otro cuadrado congruente. ¿Cuál es el área en cm2, de la parte común de estos dos cuadrados?
a) 1 cm2
|
b) 1,5 cm2
|
c) 2 cm2
|
d) 2,5 cm2
|
a)
5) Calcular el área sombreada de la siguiente figura
a) 13/2 cm2
|
b) 13 cm2
|
c) 15/2 cm2
|
d) 7,5 cm2
|
a)
6) El lado del cuadrado es 6 cm. Calcular el área de la región sombreada
a) (36-p) cm2
|
b) (44-p) cm2
|
c) 4(9-p) cm2
|
d) (36-4p) cm2
|
a)
7) El radio de la circunferencia es 2 cm. Calcular el área de la región sombreada
a) (36-p) cm2
|
b) (44-p) cm2
|
c) 4(4-p) cm2
|
d) (5-4p) cm2
|
c)
8) Si r=4 cm. Calcular el área de la región sombreada
a) 46p cm2
|
b) 44p cm2
|
c) 40p cm2
|
d) 32p cm2
|
d)
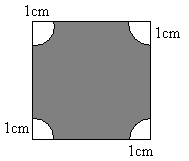
9) El lado del cuadrado es 4 cm. Calcular el área de la región sombreada
a) 4 cm2
|
b) 6 cm2
|
c) 8 cm2
|
d) 16 cm2
|
c)
10) Calcular el área de la región sombreada
a) 18 cm2
|
b) 36 cm2
|
c) 16 cm2
|
d) 49 cm2
|
b)
11) Calcular el área de la región sombreada
a) 64p cm2
|
b) 32p cm2
|
c) 16p cm2
|
d) 8p cm2
|
b)
12) El área de la región sombrea es:
a) 4 cm2
|
b) 6 cm2
|
c) 8 cm2
|
d) 10 cm2
|
c)
13) Con 625 baldosas cuadradas de 20cm de lado se desea embaldosar una sala cuadrada. ¿Cuál es largo de la sala?
a) 25 m
|
b) 5 m
|
c) 4 m
|
d) 10 m
|
b)
14) Se desea recortar un espejo de forma circular de radio 30 cm a partir de un cuadrado. ¿Cuál es el área del menor cuadrado?
a) 3600 cm2
|
b) 240 cm2
|
c) 900 cm2
|
d) 1000 cm2
|
a)
15) Calcular el área de la región sombreada
a) 16(4-p) cm2
|
b) 4(16-p) cm2
|
c) 16(5-p) cm2
|
d) 26(4-p) cm2
|
a)
16) Calcular el área de la región sombreada (corona circular) en donde

cm
a) 12p cm2
|
b) 16p cm2
|
c) 5p cm2
|
d) 4p cm2
|
a)
17) Calcular el área de la región sombreada (trapecio circular) en donde r1= 4 cm
a) 2p cm2
|
b) 4p cm2
|
c) 3p cm2
|
d) 6p cm2
|
c)
18) Si el lado del cuadrado mide 4 cm. Calcular el área de la región sombreada
a) 4(4-p) cm2
|
b) 4(p-1) cm2
|
c) 4(5-p) cm2
|
d) 4(p-2) cm2
|
a)
19) Si el lado del cuadrado mide 4 cm. Calcular el área de la región sombreada
a) 16(p-1) cm2
|
b) 4p cm2
|
c) 3p cm2
|
d) 8(p-2) cm2
|
d)
20) Si el lado del cuadrado mide 4 cm. Calcular el área de la región sombreada
a) 16(p-2) cm2
|
b) 8(p-2) cm2
|
c) 4(p-2) cm2
|
d) 2p-4 cm2
|
b)
21) Calcular el área de la región sombreada en donde d =10 cm y b =8 cm.
a) 24 cm2
|
b) 44 cm2
|
c) 48 cm2
|
d) 12 cm2
|
a)
22) El diámetro de la circunferencia es 4 cm. Calcular el área de la región sombreada
a) 8 cm2
|
b) 16 cm2
|
c) 32 cm2
|
d) 64 cm2
|
a)
23) En la figura, el perímetro del cuadrado es

El área sombreada es:
a) 4p-2
|
b) 3p-2
|
c) 2p-1
|
d) p-2
|
d)
AYALA, ORLANDO, (2006), Matemática Recreativa, M & V GRÁFIC. Ibarra, Ecuador
SUÁREZ, MARIO
BENALCÁZAR, Marco, (2002), Unidades para Producir
Medios Instruccionales en
Educación, SUÁREZ, Mario Ed. Graficolor, Ibarra,
Ecuador.
SUÁREZ, Mario, (2004), Interaprendizaje Holístico de Matemática, Ed.
Gráficas Planeta,
Ibarra, Ecuador.
SUÁREZ, Mario, (2004), Hacia un Interaprendizaje Holístico de
Álgebra y
Geometría, Ed. Gráficas
Planeta, Ibarra, Ecuador.
Autor:
Mario Orlando Suárez Ibujes

 . Hallar sus dimensiones.
. Hallar sus dimensiones. . Hallar su perímetro.
. Hallar su perímetro. //
//  ;
;  = 45º,
= 45º,  = 3a;
= 3a;  =
= = a.
= a. , sabiendo que la base es
, sabiendo que la base es  de la mayor y
que la altura es igual al tercio de la suma de las bases.
de la mayor y
que la altura es igual al tercio de la suma de las bases.



 = l2 = (4cm)2 = 16 cm2
= l2 = (4cm)2 = 16 cm2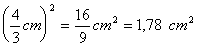
 = A
= A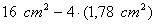
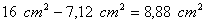


 = 4 cm ? l
= 4 cm ? l
 cm y el ? tiene un tercio de 3600
cm y el ? tiene un tercio de 3600
 ?
? 



 cm .
cm .





 cm .
cm .
 cm =
cm =  cm =
cm =  cm
cm cm
cm ??
?? 



 como indica la figura:
como indica la figura:
 ?
?  ??
?? 



 de la pizza,
de la pizza,





 cm y b =
cm y b =  cm.
cm.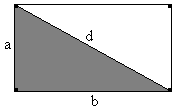




 =
= 
 cm. Calcular el área de la región sombreada
cm. Calcular el área de la región sombreada


















 cm
cm





 El área sombreada es:
El área sombreada es: